Deterministic Finite State Machine Minimization

May 8^th, 2015 automata, csharp, dotnet, theory of computation Comments

I have received a question about how to approach DFSM minimization in one of the previous posts. This is an attempt to answer that question.

What is DFSM minimization?

First, let us consider what does it mean for two DFSM to be equivalent? Imagine having two DFSM that both accept the same input symbols. You then pass all the possible inputs to those two machines. If and only if the answers are the same for all the inputs then the two machines are equivalent. That is: they accept exactly the same inputs, even though their inner workings might not be the same.

This means that there are many equivalent DFSM. For example all three DFSM in the below picture accept the same input which can be written as a regular expression (0+1)^*.

Deterministic finite state machine equivalence

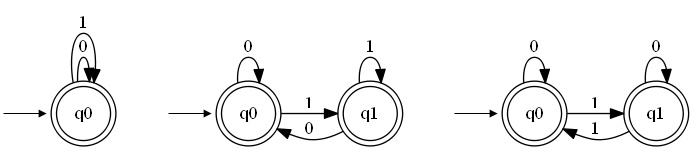
The three DFSM vary in the number of states and also in the number of the transitions. Nonetheless, I hope you will agree with me that they all accept the same input.

Powerset Construction in C#

Apr 30^th, 2015 automata, csharp, dotnet, theory of computation Comments

In the last two articles I have implemented the deterministic finite state machine (DFSM) and the non-deterministic finite state machine (NDFSM). As you probably all know the two variants are equivalent in terms of power; that is everything that can be expressed with one can also be expressed with the other. This may come as a surprise when you first hear about it, but you are soon presented with the powerset construction which converts a NDFSM into a DFSM and thus proves one part of the equivalence. The other part is trivial since DFSM is only a limited NDFSM.

Non-deterministic Finite State Machine Implementation in C#

Apr 12^th, 2015 automata, csharp, dotnet, theory of computation Comments

Last time I implemented the deterministic finite state machine (DFSM). This time I will do the same for the non-deterministic (NDFSM) one. I chose the variation without the epsilon transitions and will leave that for exercise if someone might find it intriguing.

The only difference between the DFSM and NDFSM is that while the DFSM can only have a single transition for a given state and input symbol the NDFSM is not limited in that regard. It can have multiple transitions for a given state and input symbol.

Deterministic Finite State Machine Implementation in C#

Aug 13^th, 2014 automata, csharp, dotnet, theory of computation Comments

While I was working at the Faculty of Computer and Information Science I have implemented many of the standard algorithms from the famous Cormen’s Introduction to Algorithms. Since I was a part of the Laboratory for algorithms and data structures that is to be expected. However, I have never implemented many of the great results from the Theory of Computation.

This is why I decided to implement the finite state machine and the Turing machine in C# as an exercise. In this blog post I will start with the easier of the two, the finite state machine (FSM).

Excel VSTO RGB Color Bug

Aug 5^th, 2014 color, excel, excel bug Comments

One of the strangest bugs I found in VSTO for Excel is the one that deals with assigning colors to the RGB property of the ChartFormat object. The ChartFormat object is used in multiple places of Excel. Let’s look at an example:

Series series = Globals.ThisAddIn.Application.Selection;
series.Format.Fill.ForeColor.RGB = Color.Red.ToArgb();

For brevity’s sake let’s suppose that we have a series of a chart selected and we run the code above. One would expect that the color of the selected series would be set to red, but what happens is this:

Chart

Mitja Bezenšek

Writing about software development, agile techniques, C#, Excel and occasional random thoughts.