In the last two articles I have implemented the deterministic finite state machine (DFSM) and the non-deterministic finite state machine (NDFSM). As you probably all know the two variants are equivalent in terms of power; that is everything that can be expressed with one can also be expressed with the other. This may come as a surprise when you first hear about it, but you are soon presented with the powerset construction which converts a NDFSM into a DFSM and thus proves one part of the equivalence. The other part is trivial since DFSM is only a limited NDFSM.

Powerset construction algorithm

Like I discussed in my previous blog post, the only difference between the DFSM and the NDFSM is that the DFSM does not allow multiple transitions for a given state and symbol. If we wish to transform a NDFSM into a DFSM we need to remove these multiple transitions. We can achieve this by combining all the states that we can reach with a given symbol from a given state into a new state which is a set of all the reachable states.

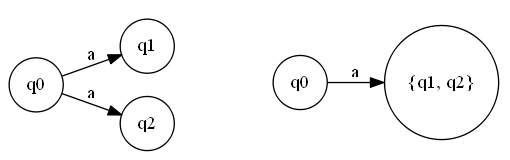
As you can see on the left side of the above picture we can reach states q1 and q2 from the state q0 using the symbol a. This means that the state q0 has multiple transitions defined for the symbol a and we wish to get rid of these multiple transitions. The powerset construction combines states q1 and q2 into a new state that is the set of these two states as can be seen on the right side of the picture. The new state is denoted as {q1, q2}. When we do this transformation for the combined states, like the {q1, q2}, we need to look at the transitions for all the states that make this combined state, in this case q1 and q2.

The good news is that this does exactly what we need: it gets rid of the multiple transitions. The bad news though is that in the worst case the number of states explodes and we end up with the states that are all the possible subsets of our original set of states.

Ouch.

So how would we approach this constructions programmatically? Probably the easiest way would be to keep a queue of states that we wish to process. The initial queue would only contain the starting states. We would then add all the possible states that are reachable from the starting states. If there are multiple transitions from a state with a given symbol we would create a new combined state like described in the previous paragraph and add it to the queue. For the symbols that only have one transition we would just add the ending state of the transition to the queue. We would then remove a state from the queue and repeat the described algorithm until we empty the queue.

Determining the finish states of the DFSM machine is easy. The finish states will be all the finish states of the original NDFSM plus the combined states that have a least one of the finish states as one of their elements.

During the execution of the algorithm we would of course need to keep track of the already processed states and the transitions between them so that we can construct our NDFSM.

Here is one possible implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

public static DFSM Convert(NDFSM nd){
  var Q = new List<string>();
  var Sigma = nd.Sigma.ToList();
  var Delta = new List<Transition>();
  var Q0 = nd.Q0.ToList();
  var F = new List<string>();
  
  var processed = new List<string>();
  var queue = new Queue<string>(Q0);
  while (queue.Count > 0){
     var setState = queue.Dequeue();
     processed.Add(setState);
     Q.Add(setState);

      var statesInCurrentSetState = setState.Split(',').ToList();
      foreach (var state in statesInCurrentSetState){
          if (nd.F.Contains(state)){
              F.Add(setState);
              break;
         }
      }
      var symbols = nd.Delta
         .Where(t => statesInCurrentSetState.Contains(t.StartState))
         .Select(t => t.Symbol)
         .Distinct();
      foreach (var symbol in symbols){
         var reachableStates =
            nd.Delta
               .Where(t => t.Symbol == symbol &&
                           statesInCurrentSetState.Contains(t.StartState))
               .OrderBy(t => t.EndState)
               .Select(t => t.EndState);
         var reachableSetState = string.Join(",", reachableStates);

         Delta.Add(new Transition(setState, symbol, reachableSetState));

         if (!processed.Contains(reachableSetState)){
            queue.Enqueue(reachableSetState);
         }
      }
  }
  return new DFSM(Q, Sigma, Delta, Q0, F);
}

Conclusion

This algorithm was actually easier to implement than I thought. I thought that I would need to generate the powerset and then all the possible transitions between all the states. I took a different approach which only goes through the reachable states and only generates the states of the powerset that are actually needed. The algorithm turned out much simpler and on top of that it also produces a better results since the unreachable states are pruned away!

The source code is available at Github.